Рождение виртуальной клеточной биологии
05 сентября 2012
Рождение виртуальной клеточной биологии
- 3023
- 0
- 2
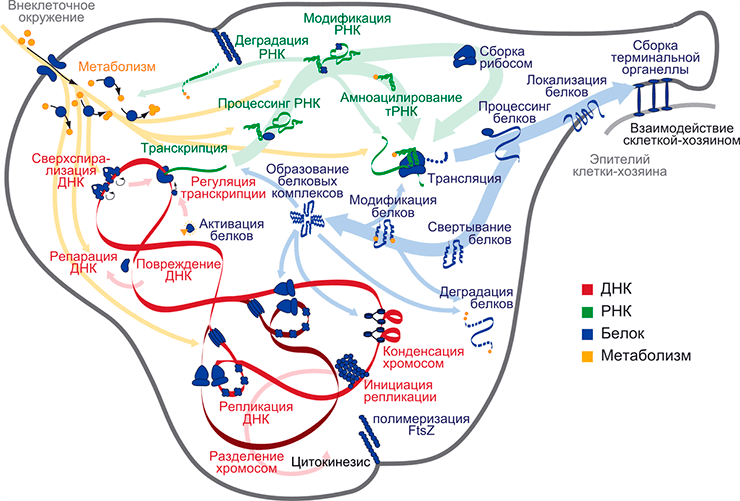
Модель клетки Mycoplasma genitalium как целого, которая состоит из 28 субмоделей различных клеточных процессов. Субмодели сгруппированы по категориям: ДНК, РНК, белки и метаболизм. Субмодели связаны друг с другом через общие метаболиты, РНК, белки и хромосомальную ДНК, что показано стрелками соответствующих цветов. Рисунок в полном размере.
-
Автор
-
Редакторы
Статья на конкурс «био/мол/текст»: Системная биология сулит нам понимание жизни на принципиально новом уровне, которого невозможно достичь без разработки количественных моделей клетки как целого и проверки сделанных ими предсказаний. В июльском выпуске журнала Cell за 2012 год опубликована работа «Вычислительная модель клетки как целого предсказывает фенотип из генотипа», в которой Карр и соавторы представляют первую комплексную динамическую вычислительную модель бактерии, учитывающую все её компоненты и взаимодействия между ними.
Конкурс «био/мол/текст»-2012
Эта статья представлена на конкурс научно-популярных работ «био/мол/текст»-2012 в номинации «Лучшее новостное сообщение».
Спонсор конкурса — дальновидная компания Thermo Fisher Scientific.
Научные дисциплины должны время от времени бросать вызов тем стандартам, которым соответствует их уровень понимания предмета. Безусловным стандартом в классической механике является способность предсказать динамическое поведение физической системы. Достигнет ли биология когда-либо такого же уровня понимания живой системы, пусть даже для отдельно взятой клетки? Похоже, что именно сейчас настало время проверить наши знания о клетке, создав математическую модель всех клеточных процессов с использованием всех известных нам данных. Дьявол в этом проекте кроется в тысячах деталей, которые должны быть учтены до всех нюансов, чтобы в совокупности получить полную модель клетки как целого с приемлемой точностью. В недавнем выпуске одного из самых авторитетных биологических журналов Cell [1] описана полная компьютерная модель бактерии Mycoplasma genitalium, которая учитывает влияние всех известных генов и их продуктов и позволяет провести моделирование полного клеточного цикла.
M. genitalium уже стала классикой синтетической биологии (см. «Смыслы „жизни“» [12]). Геном этой бактерии, признанный минимальным для свободноживущего микроорганизма, был в несколько этапов синтезирован «в пробирке» (см. «Геном, собранный вручную» [13]). А на родственной микоплазме провели работу, окрещенную в СМИ «сотворением жизни» (см. «Жизнь в эпоху синтетической жизни» [14]). — Ред.
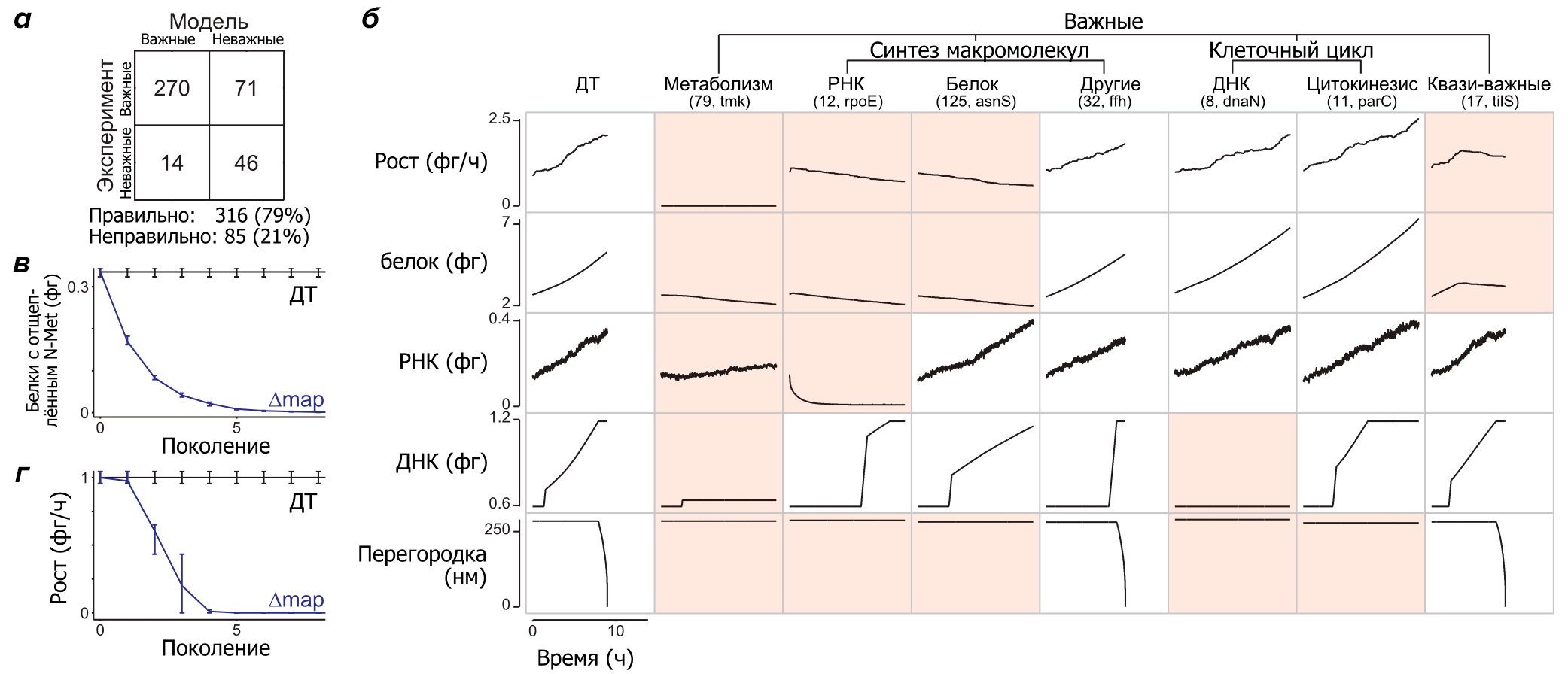
Рисунок 1. Модель выявляет молекулярные патологии, лежащие в основе фенотипов с одним удаленным геном. а — Сравнение важности (существенности) генов для жизни клетки, в соответствии с предсказаниями модели и данными эксперимента [11]. Предсказания модели опираются как минимум на пять независимых расчетов каждого из штаммов с одним удаленным геном. б — Штаммы с одним удаленным геном группируются в фенотипические классы (столбцы), в соответствии с их способностью расти, синтезировать белок, РНК, ДНК и делиться (показана длина перегородки, сокращение которой приводит к делению клетки). В столбцах показана динамика одной репрезентативной клетки для каждого класса важных генов. Штаммы с удаленными несущественными генами не показаны. Красным цветом показана динамика, которая существенно отличается от клеток дикого типа (ДТ). В скобках приведено число генов в каждой категории название удаленного гена в репрезентативной клеточной модели. в и г — Вырождение клеток и разбавление белков с отщеплённым N-концевым метионином (в) в клетках с удаленным геном метионин аминопептидазы (map, MG172) вызывает замедленный рост клеток (г). Синим и черным цветами показаны данные моделирования для штамма с удаленным геном map (Δmap) и для клеток дикого типа (ДТ). Вертикальные линии указывают величину стандартного отклонения.
Предложенная авторами модель — это первая действительно всеобъемлющая попытка построить модель функционирования свободноживущего микроорганизма, которая достойна похвалы за свою исключительную смелость. Это гигантская задача, которая включает интерпретацию и объединение огромных объемов данных, многие из которых были взяты из других близких бактерий, таких как Mycoplasma pneumonia и Escherichia coli. Можно спорить о том, действительно ли доступная глубина и детальность наших знаний о работе отдельных элементов достаточна для того, чтобы в настоящий момент времени пробовать построить полную модель клетки. Бесспорно, многие скажут, что скудность и фрагментарность наших знаний, даже в отношении организма, геном которого близок к минимально возможному, заранее обрекают любую попытку подобного рода на поражение. Абсолютно точная, детальная и подробно проработанная математическая модель, безусловно, является мечтой весьма отдаленного будущего. Тем не менее, в свете предложенной модели более уместным выглядит следующий вопрос: действительно ли мы уже знаем достаточно, чтобы попытаться провести грубое моделирование клетки и получить какие-либо нетривиальные результаты? Ответить на этот вопрос можно, только построив такую модель клетки, которая дает проверяемые предсказания. Это именно то, что сделали авторы, создав черновой набросок, к которому уже можно адресовать вопросы и получать ответы при помощи количественных моделей в масштабе целой клетки.
Модель, предложенная американскими биологами [1], — это не первая попытка создать количественную предсказательную компьютерную модель масштаба целой клетки. Прежние попытки основывались на нелинейных дифференциальных уравнениях для моделирования биологических сетей [2] или моделировании, основанном на ограничениях, таких как анализ баланса реакций (Flux Balance Analysis, FBA) [3] . Из всех предыдущих методов моделирования сетей клеточной регуляции и метаболизма, метод FBA заслуживает особого внимания вследствие широкого спектра успешных применений этого семейства методик. Модели, основанные на ограничениях, доказали свою пользу и качественное согласие с экспериментом в различных приложениях: от предсказания и объяснения эволюционных траекторий до метаболической инженерии [4]. Несмотря на многочисленные успехи, эти алгоритмы вынуждены ограничиваться некоторым подмножеством всех процессов клетки, поскольку до сих пор отсутствует методика расчета, применимая для моделирования всего разнообразия реакций и взаимодействий, происходящих в живой клетке. В дополнение к этому, метод моделирования, основанный на ограничениях, дает в качестве ответа стационарное состояние клетки, а вовсе не ее динамическую эволюцию, хотя в последнее время были сделаны определенные усилия, чтобы включить FBA в моделирование динамических процессов [5].
Общие и довольно фундаментальные сведения о мультимасштабном моделировании биологических процессов можно найти в статье «Пространственно-временное моделирование в биологии» [15]. — Ред.
Для того чтобы построить модель разнородных клеточных процессов, которые происходят в живых клетках на разных масштабах времени, авторы статьи в Cell [1] используют оригинальную модульную структуру данных, в которой многочисленные процессы живой клетки развиваются и взаимодействуют друг с другом. Модули, каждый из которых представляет собой отдельный класс процессов (например, транскрипция или метаболизм) разработаны, параметризованы и протестированы независимо друг от друга; в конечной модели они описывают вовлеченные в них компоненты на разных уровнях детализации. Модули взаимодействуют между собой и обмениваются переменными (которые все вместе описывают внутреннее состояние клетки) с интервалом в одну секунду; развитие этой модели во времени позволяет выполнить моделирование всего клеточного цикла M. genitalium. Модель оказывается весьма точной по ряду ключевых пунктов; авторы показывают, что их модель дает значения концентраций метаболитов, которые в пределах порядка величины совпадают с наблюдаемыми в живых клетках. Кроме того, модель позволяет предсказать незаменимость генов M. genitalium с точностью 80% (рис. 1). Не меньше впечатляет то, что эта модель предлагает оригинальную гипотезу регуляции длительности клеточного цикла Mycoplasma: репликация генома, в конечном счете, лимитируется синтезом дезоксирибонуклеотид трифосфатов (дНТФ); в результате клетки, в которых ранние стадии клеточного цикла заняли больше времени, догоняют тех, кто запустил репликацию раньше, используя бóльшую концентрацию накопленных дНТФ во время репликации, уменьшая тем самым разброс общей длительности клеточного цикла внутри популяции (рис. 2).
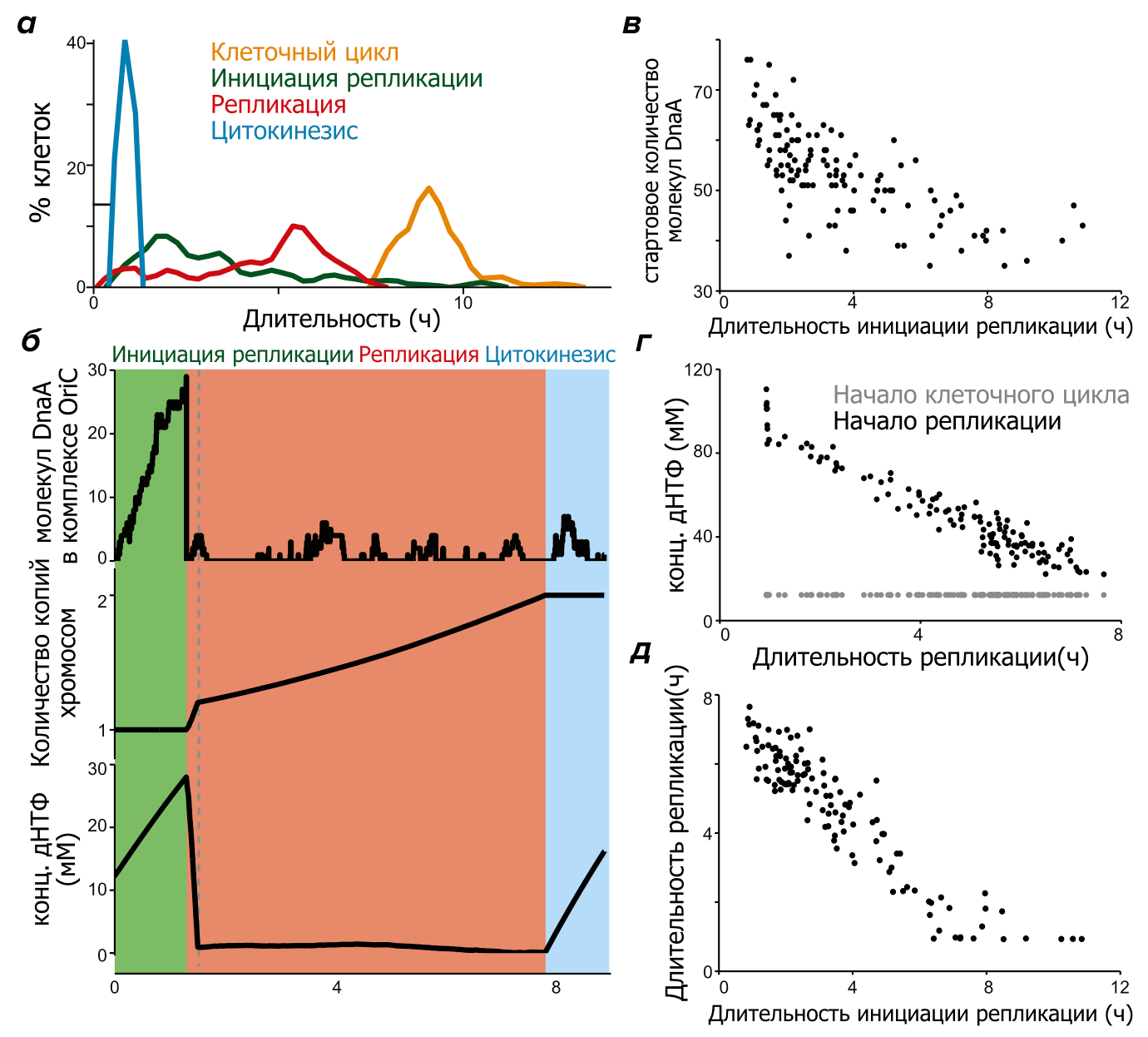
Рисунок 2. Предсказание длительности клеточного цикла, сделанное моделью клетки как целого. а — Распределение длительности трех фаз клеточного цикла и всего клеточного цикла по 128 независимым клеточным траекториям. б — Динамика количества макромолекул в одном выбранном моделировании клетки. Наверху: размер комплекса DnaA, который собирается в сайте инициации репликации OriC (в мономерах DnaA); посередине: количество копий хромосомы; внизу: концентрация дНТФ в цитоплазме клетки. Количество этих макромолекул напрямую связано с длительностью ключевых стадий клеточного цикла. в — Корреляция между начальной концентрацией DnaA в клетке и длительностью стадии инициации репликации клеточного цикла по тем же 128 клеточным траекториям, что показаны на рисунке а. г — Корреляция концентрации дНТФ (на момент начала клеточного цикла и на момент начала репликации ДНК) для тех же 128 клеточных траекторий in silico что и на рисунке а. д — Корреляция между длительностью инициации репликации и длительностью репликации для тех же 128 клеточных траекторий in silico.
В свете представленного научного достижения важно ответить на два ключевых вопроса: (1) что мы ожидаем узнать из математической модели клетки как целого и (2) как такая модель должна взаимодействовать с другими областями биологии. Эти вопросы иллюстрирует рисунок 3, из которого видно, что современная биология находится на перекрестке трех направлений: качественные принципы, лежащие в основе организации живой материи; масштабные высокопроизводительные эксперименты, которые поставляют систематизированные количественные результаты и узкоспециальные модели конкретных систем и процессов клетки, полученные в результате специализированных исследований. Количественная модель клетки как целого обещает в перспективе принципиальную возможность объединить эти разрозненные источники информации. В краткосрочной перспективе развитие и оптимизация подобных моделей сама по себе является серьезным вызовом; ученые, разрабатывающие эти модели, могут воспользоваться любым расхождением между их предсказаниями и известными экспериментальными фактами для того, чтобы уточнить структуру и содержание своих моделей. Мы можем себе представить два основных типа предсказаний, которые могут быть практически полезны:
- Открытие новых принципов организации, которые помогут собрать воедино наши знания о биологических системах («физическая перспектива»).
- Развитие достаточно точных вычислительных моделей, которые способны заменить, по крайней мере, предварительные стадии скрининга веществ в биоинженерии («инженерная перспектива»).
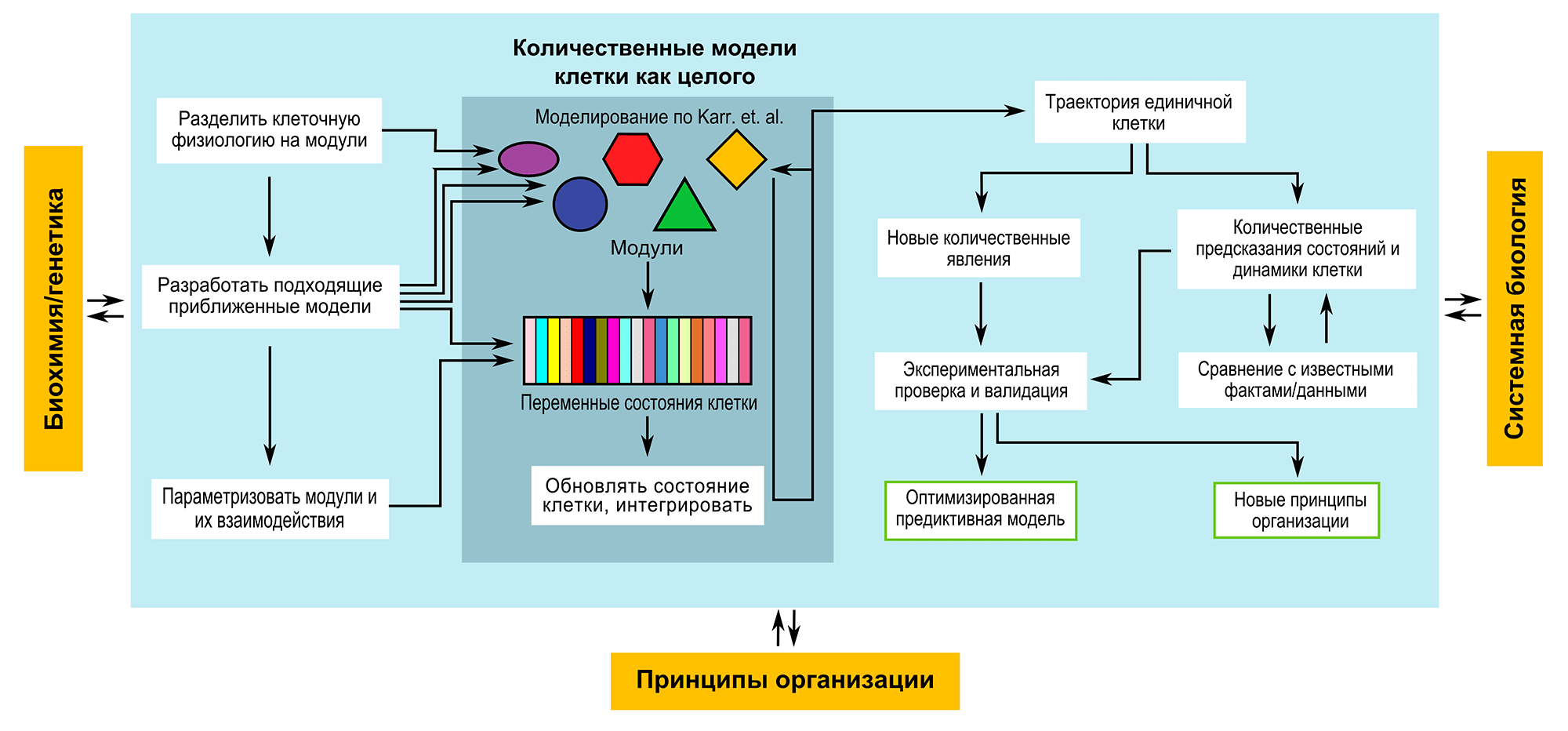
Рисунок 3. Роль моделирования клетки как целого в современной биологии. Сформировавшись, модель клетки как целого будет объединять концептуальные знания, экспериментальные данные и модели поведения специфических систем клетки (в качестве примера показаны детали моделирования из [1]); результатом такого моделирования будут количественные предсказания значений неизвестных параметров и качественная информация о новых, ранее не наблюдавшихся, моделях поведения. На этапе обучения основное внимание теоретиков должно быть сконцентрировано на уточнении модели через петлю обратной связи путем сравнения предсказаний с экспериментами — как со старыми, так и со специально поставленными новыми. Затем вычислительные модели позволят выдвигать новые, проверяемые гипотезы о принципах организации живой клетки. В дополнение к этому, количественные предсказания усовершенствованных моделей клетки будут исключительно полезны в биоинженерии.
Уникальный потенциал, который кроется в моделировании всех систем клетки — это способность проникнуть в детали процессов, которые невозможно изучить экспериментально. Действительно, такие модели могут дать исследователю неограниченно подробные траектории развития единичных клеток, включая все параметры их внутреннего состояния, которые можно будет легко изменить для того, чтобы изучить любой интересующий нас феномен.
Чрезвычайно сложная и масштабная модель, построенная авторами работы [1], — это ключевой шаг на пути создания практичных и надежных методов моделирования клетки. Особенно впечатляет то, что эта изощренная модель дает нам не только приблизительное количественное согласие с разнообразными экспериментально измеренными параметрами, но и новое понимание механизмов регуляции биологических процессов. Тем не менее, мы должны особо подчеркнуть, что эта модель далека от идеальной «платонической» модели M. genitalium. Каждый модуль, входящий в модель, наверняка может быть раскритикован с точки зрения математического содержания, однако на настоящий момент этот подход достигает оптимального баланса между реалистичностью, вычислительной сложностью и количеством свободных параметров. Как обращают внимание сами авторы, данная модель представляет собой лишь первый черновой набросок, скорее важный в качестве отправной точки для дальнейшего уточнения, чем как модель сама по себе.
В дальнейшем исследователям предстоит критически изучить все ошибки данной модели и определить, какие изменения структуры и параметров требуется внести для их устранения; по мнению авторов, чрезвычайно важно расширить модель на более полно изученные организмы, такие как E. coli. В дополнение к этому, для построения законченной реконструкции клетки разработчики моделей должны уделить особое внимание тем упрощениям, принятым в работе [1], которые заведомо не выполняются в реальных клетках. Сюда относятся наличие широко распространенных антисмысловых транскрипций в геноме [6], эффекты пространственной гетерогенности [7] и многофункциональность ферментов [8]. Также пока еще не вполне ясно, насколько уязвимы такие масштабные клеточные модели по отношению к неопределенностям в значениях параметров, которая характерна для моделей системной биологии [9]. Нужно выяснить, насколько хорошо общее поведение клетки будет предсказываться исходя из параметров, полученных в различных моделях, и до какой степени можно будет полагаться на индивидуальные переменные состояния клетки, даже если общая картина клетки как целого будет выглядеть корректной.
По материалам редакционного материала Cell [10]. Первоначально перевод был опубликован на сайте ИБХ РАН.
Литература
- Jonathan R. Karr, Jayodita C. Sanghvi, Derek N. Macklin, Miriam V. Gutschow, Jared M. Jacobs, et. al.. (2012). A Whole-Cell Computational Model Predicts Phenotype from Genotype. Cell. 150, 389-401;
- M. Castellanos, D. B. Wilson, M. L. Shuler. (2004). A modular minimal cell model: Purine and pyrimidine transport and metabolism. Proceedings of the National Academy of Sciences. 101, 6681-6686;
- Jeffrey D Orth, Ines Thiele, Bernhard Ø Palsson. (2010). What is flux balance analysis?. Nat Biotechnol. 28, 245-248;
- Adam M Feist, Bernhard Ø Palsson. (2008). The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat Biotechnol. 26, 659-667;
- Jong Min Lee, Erwin P. Gianchandani, James A. Eddy, Jason A. Papin. (2008). Dynamic Analysis of Integrated Signaling, Metabolic, and Regulatory Networks. PLoS Comput Biol. 4, e1000086;
- James E. Dornenburg, Anne M. DeVita, Michael J. Palumbo, Joseph T. Wade. (2010). Widespread Antisense Transcription in Escherichia coli. mBio. 1;
- Elijah Roberts, Andrew Magis, Julio O. Ortiz, Wolfgang Baumeister, Zaida Luthey-Schulten. (2011). Noise Contributions in an Inducible Genetic Switch: A Whole-Cell Simulation Study. PLoS Comput Biol. 7, e1002010;
- Olga Khersonsky and Dan S. Tawfik. (2010). Enzyme Promiscuity: A Mechanistic and Evolutionary Perspective. Annu. Rev. Biochem.. 79, 471-505;
- Ryan N. Gutenkunst, Joshua J. Waterfall, Fergal P. Casey, Kevin S. Brown, Christopher R. Myers, James P. Sethna. (2007). Universally Sloppy Parameter Sensitivities in Systems Biology Models. PLoS Comput Biol. 3, e189;
- Peter L. Freddolino, Saeed Tavazoie. (2012). The Dawn of Virtual Cell Biology. Cell. 150, 248-250;
- J. I. Glass, N. Assad-Garcia, N. Alperovich, S. Yooseph, M. R. Lewis, et. al.. (2006). Essential genes of a minimal bacterium. Proceedings of the National Academy of Sciences. 103, 425-430;
- Смыслы «жизни»;
- Геном, собранный вручную;
- Жизнь в эпоху синтетической жизни;
- Пространственно-временное моделирование в биологии.