Хаос в мозге
25 мая 2017
Хаос в мозге
- 3139
- 3
- 9
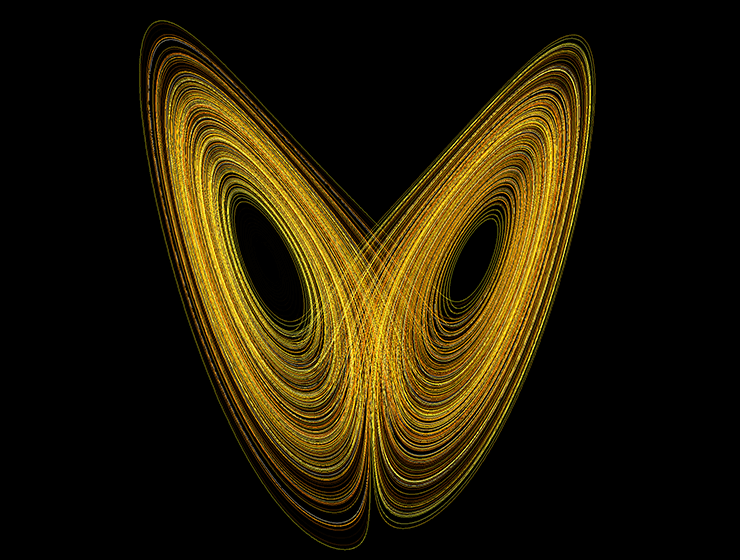
Артистическое представление аттрактора Лоренца. Показаны траектории движения точки, скорость которой описывается нелинейными дифференциальными уравнениями. Цвет соответствует скорости движения.
-
Автор
-
Редакторы
Если бы мы могли увидеть активность всех нейронов коры нашего мозга, мы бы, скорее всего, решили, что она совершенно беспорядочна и случайна. Однако это только на первый взгляд. Недавно биологи выяснили, что внешне беспорядочное поведение нейронов в коре можно объяснить с помощью известного в физике феномена динамического хаоса (который, впрочем, далек от полнейшего беспорядка). Вооружившись новыми знаниями, они даже научились управлять небольшим виртуальным роботом. Так что же такое хаос и какое отношение имеет он к работе нейронов мозга?
Нейробиологов давно интересует решение парадокса: как из отдельных ненадежных элементов, таких как нейроны, строится наша в высшей степени надежная нервная система? Отдельный нейрон, как и любая другая клетка организма, не вечен. Если вы случайно ударитесь головой, будьте уверены, что какое-то количество нервных клеток при этом погибнет. Однако в большинстве случаев это не приводит к тому, что вы больше не сможете ходить, разговаривать, думать или не вспомните свое имя и прочую важную информацию. Каким же образом мозгу удается надежно сохранять функцию, даже если какие-то из элементов больше не работают?
Возможно, дело вот в чём: функция мозга опирается на активность не одного нейрона, а большой их группы. Таким образом, если какие-то элементы сети выйдут из строя, всегда найдутся другие, которые смогут поддержать функцию. Но как можно построить сеть таким образом и какую активность она должна проявлять, чтобы добиться желаемого результата?
Если взглянуть на активность отдельных нейронов в коре мозга близких нам макак, то окажется, что нервные импульсы, или спайки, генерируются достаточно случайно (рис. 1) [1]. Причем эта «случайность» наблюдается как в состоянии покоя, когда кора мозга непосредственно не занимается обработкой какой-либо информации, так и при выполнении определенной функции — например, во время ответов зрительной коры на предъявление стимула (макака видит фрукт). А ведь, казалось бы, упорядоченное действие должно управляться упорядоченными импульсами...
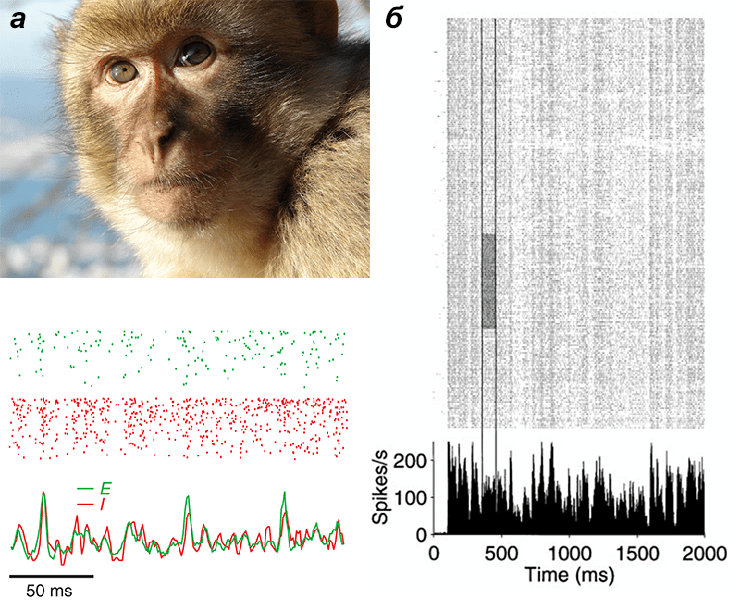
Рисунок 1. Вариабельность ответов отдельных нейронов в коре мозга. а — Записи активности отдельных нейронов зрительной коры макаки при предъявлении одного и того же зрительного стимула несколько раз. Сверху показана активность клеток, где каждая точка соответствует отдельному спайку. Снизу — средняя частота спайков. б — Активность сети нейронов в математической модели коры. Зеленым показана активность возбуждающих нейронов (E), красным — активность тормозных нейронов (I). На обеих картинках каждая точка соответствует моменту генерации спайка.
Современные биологи активно используют математику для того, чтобы лучше понять происходящее в живых организмах [2]. И нейробиологи здесь исключением не стали. Математически время генерации импульсов можно описать с помощью процесса Пуассона: момент генерации нервного импульса наступает случайно и не зависит от того, когда произошли предыдущие импульсы. Схожим образом приходят автобусы на остановку: частота их рейсов, вроде бы, примерно известна, но когда именно получится поехать, предсказать сложно — бывает и так, что на остановке можно увидеть сразу несколько автобусов, которые прибывают один за другим. Так же случайно, но с определенной интенсивностью, срабатывают нейроны коры.
Это приводит к тому, что на один и тот же стимул ответ будет в каждом случае разным [3]. Для сравнения: при нажатии одной и той же последовательности клавиш на компьютере вы всегда будете получать одинаковый текст. Как же тогда мозг понимает, что стимул один и тот же? Если в коре мозга действительно есть представление о стимуле, то как оно выглядит?
Сестра Хаос
Карл ван Врисвик и Хаим Сомполински в 1990-х предложили объяснение кажущейся случайной активности сети нейронов с помощью элегантной модели [4]. Оказалось, что в больших сетях (около 10 000 клеток), связанных случайными возбуждающими и тормозными связями, хаотическая активность возникает сама по себе при соответствующих условиях. В таком случае каждая клетка из окружающей ее сети получает «вход», похожий на шум [5]. Такое явление хорошо известно в физике как динамический хаос.
Установлено, что если в системе есть более трех взаимодействующий друг с другом элементов, при определенных условиях ее поведение может напоминать случайное, даже если никакой случайности в уравнениях нет. Такое поведение называется хаотическим. В этом режиме активности поведение нейронов сети крайне чувствительно к начальным условиям. Это значит, что даже небольшое изменение потенциала отдельного нейрона приводит к совершенно другому состоянию сети уже в ближайшем будущем — такие вещи абсолютно нормальны для хаотических процессов.
Представим себе процесс, описываемый достаточно простым математическим уравнением: значение функции в определенный момент времени однозначно задается значением на предыдущем шаге. Выберем два начальных (в момент времени t=0) состояния: x1(t=0) = 0,5 и x2(t=0) = 0,5000000000001. Совсем небольшое различие, не правда ли? А теперь каждое последующее значение x(t+1) будем рассчитывать как x(t+1) = 1,9−x2(t) на основании предыдущего x(t). И вот что удивительно: даже такое небольшое различие условий на старте приводит к совершенно разным траекториям x1 и x2 уже в ближайшем будущем (рис. 2)! Именно это и называется чувствительностью к начальным условиям (или неустойчивостью), которая ведет к быстрому расхождению траекторий во времени.
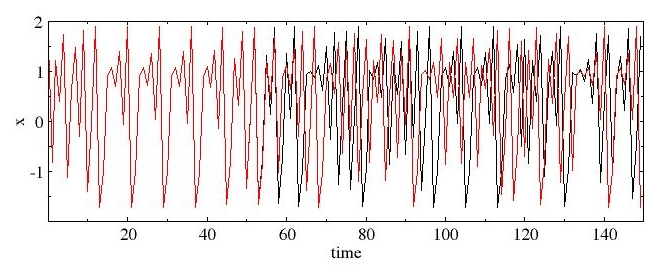
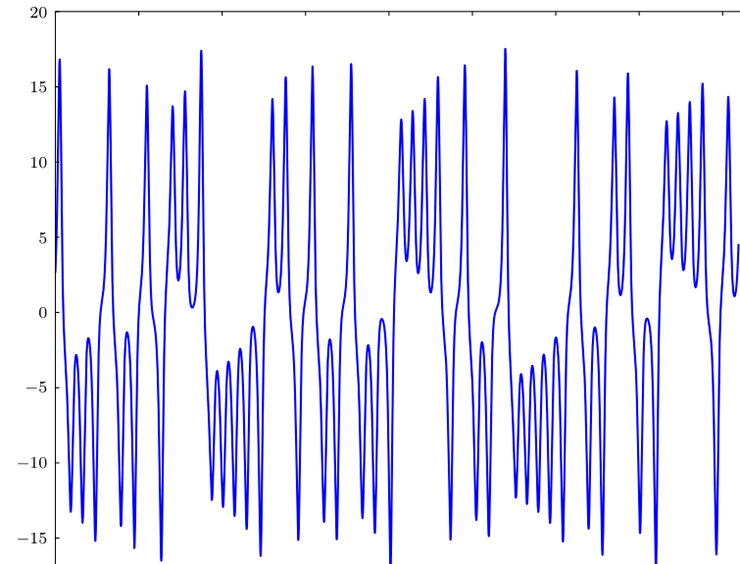
Рисунок 2. Чувствительность хаотической системы к начальным условиям. Разными цветами показаны две траектории решений уравнения Гребоги, которое используют при описании поведения плазмы. Каждая следующая точка (в момент времени t+1) получена из предыдущей (в момент времени t) по закону: x(t+1) = 1,9−x2(t). Красная линия — x(t=0) = 0,5000000000001, черная — x(t=0) = 0,5.
сайт complex.upf.es
В случае если есть только одна переменная x(t), такое расхождение траекторий довольно просто представить (рис. 2). Однако в более сложных системах с большим числом элементов, как например в сети из 10 000 нейронов, такое поведение уже гораздо сложнее визуализировать, поэтому часто ученые используют различные метафоры.
С помощью геометрии объяснить хаос можно примерно так. Представьте, что траектория системы — это траектория шарика, падающего на седло. Немного задержавшись на седле, он скатывается вниз налево или направо на другое седло, а затем на еще одно, и так далее. При этом на пути шарика не будет ни одной ямы, где бы он мог застрять. Таким образом, он будет вечно падать по сложной траектории. Несмотря на то что количество седел будет постоянным, каждый раз он будет падать на седло и скатываться в разные стороны. Поэтому движение такого шарика во времени может казаться случайным. Если говорить о хаосе в системе, таких седел имеется огромное количество, поэтому предсказать движение шарика довольно сложно (рис. 3).
Классический пример хаотической системы в физике — аттрактор Лоренца (забавно, что у него даже есть аккаунт «ВКонтакте»). Аттракторами в математике называют устойчивые решения в системах уравнений; в случае хаотического поведения аттракторы называют странными. Например, если вы упали в яму и не можете из нее выбраться, эта яма является для вас аттрактором. Уравнения, которыми описывается аттрактор Лоренца, появились при изучении конвекции в атмосфере. В 1960-х ученый Эдвард Лоренц обнаружил, что при определенном значении параметров в уравнениях, описывающих конвекцию в жидкости, возникает необычное поведение. Траектории отдельных координат могут казаться случайными и шумными, но, если взглянуть на траектории в трехмерном пространстве, они уже не кажутся случайными и даже напоминают бабочку. Это важная особенность динамического хаоса: во времени всё выглядит крайне шумным и случайным, но если посмотреть на форму траекторий, то они совсем не кажутся беспорядочными (рис. 3). Именно это отличает динамический хаос от по-настоящему случайной активности.
Несмотря на то что хаотические траектории кажутся случайными, всё движение в целом подчиняется более сложному порядку. Это значит, что двигаться система может только в пределах аттрактора («бабочка»), то есть ее движение не так уж и случайно.
Теорию хаоса активно используют для описания поведения сложных систем, состоящих из большого числа элементов. Например, в расчетах формы кораблей и самолетов при учете турбулентности в жидкостях и газах, состоящих из большого числа молекул.
Перейдем к мозгу
Но какое же отношение хаос имеет к мозгу? Особенность хаоса в таких больших системах, как нейронная сеть, — его устойчивость. Это значит, что поведение системы будет очень похожим даже в случае разных значений параметров. Главное, чтобы каждый нейрон приобрел довольно большое количество возбуждающих и тормозных связей, тогда общий вход проще сбалансировать так, чтобы в среднем возбуждение и торможение было скомпенсировано. При этом конкретное значение силы связей может быть не столь важным для поведения системы в целом. Более того, если нейронов достаточно много, то какую-то часть из них можно даже удалить — динамика такой сети сильно не изменится.
У хаоса в сети нейронов очень богатое поведение. Иными словами, в ней постоянно возникают новые и новые паттерны активности, в которых можно найти практически любые комбинации, ограниченные формой аттрактора. Активность настоящих нейронов можно визуализировать с помощью кальциевого имиджинга, позволяющего увидеть «случайные» разряды отдельных нейронов (см. видео 1).
Видео 1. Активность зрительной коры мыши при предъявлении стимула в виде движущихся полос. Вспышки света соответствуют спайкам отдельных нейронов
Порядок из хаоса
Даже если теория хаоса объясняет общий принцип активности нейронов коры, не понятно, как можно использовать непредсказуемые ответы сети для выполнения точных вычислений. Из-за чувствительности к начальным условиям ответы сети на один и тот же стимул будут разными. Если в сети всё время возникает неповторимая сложная активность в ответ на один и тот же стимул, как вообще это может быть полезным?
Оказалось, что хаотические сети нейронов можно научить генерировать заданные динамические ответы на определенные стимулы. Один из алгоритмов предложили Ларри Эбботт и Дэвид Суцилло [6]. Он позволяет обучать сеть, которая изначально находится в хаотическом режиме, формировать строго определенные паттерны активности за счет изменения связей между нейронами. С помощью такой сети можно даже управлять небольшим виртуальным роботом, научив одну и ту же сеть и ходить, и бегать (рис. 4, видео 2 и 3).
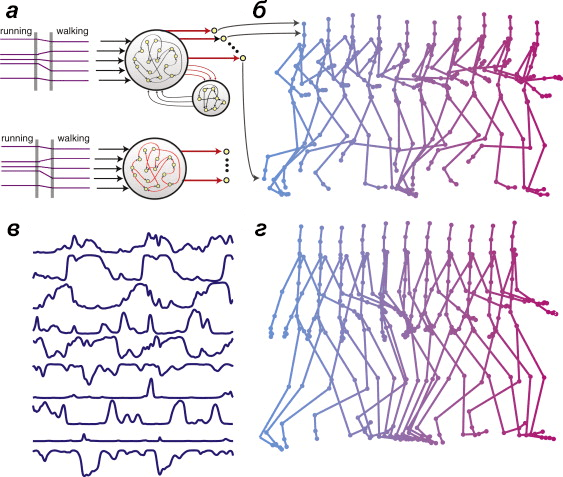
Рисунок 4. Активность хаотической сети, управляющая движением робота. а — Архитектура рекуррентной сети, которую обучили управлять движением робота во время ходьбы и бега (см. также видео 2). в — Пример хаотической активности нейронов сети, где показана частота импульсов. б, г — Движения виртуального робота в случае бега или ходьбы. Синим показаны более ранние движения, розовым — более поздние.
Видео 2. Ходьба виртуального робота
Видео 3. Бег виртуального робота
С биологической точки зрения важно, что при таком режиме работы сети сохраняется вариабельность ответов (рис. 4в), как в естественных нейронных сетях коры мозга, то есть ответы отдельных нейронов каждый раз должны быть немного разными. В таком случае ключевым становится правильное считывание активности сети. Обучать необходимо лишь определенные синапсы, а не всю сеть в целом. Еще одна важная особенность такой системы — обучение в режиме реального времени. Как и в мозге, у сети нейронов нет времени ждать, пока вся доступная информация будет получена. Обучение должно происходить на ходу. Если музыкант будет долго думать, какую ноту сыграть следующей, никакой музыки не получится.
Некоторые ученые, как например Софи Денев в Париже, придумывают алгоритмы обучения таких сетей нейронов, которые, с одной стороны, характерны для живых систем, а с другой — позволяют вычислять что-то полезное (например, аппроксимировать функции). Это дает возможность хаотическим сетям нейронов стабильно чем-то управлять.
Конечно, не все нейроны в мозге генерируют импульсы хаотически, так работают в основном нейроны коры. Многих нейробиологов за повышенное внимание именно к этой части мозга, по словам Кристофа Коха, можно называть кортикальными шовинистами. Но всё дело в том, что именно в этой эволюционно новой структуре мозга выполняются самые сложные вычисления, которые позволяют нам и другим млекопитающим быть такими умными.
Слово «хаос» (греч. χαος) в Древней Греции означало первичное состояние Вселенной до сотворения материи и пространства. Это похоже на кору мозга ребенка, который при рождении не знает о мире ничего, но постепенно обучается, что приводит к закреплению определенных паттернов активности. Это позволяет нам говорить, думать и совершать осмысленные действия. Рано или поздно ученые объяснят, как происходят эти процессы на уровне отдельных нейронов, и тогда мы сможем управлять ими успешнее.
Литература
- Shadlen M.N. and Newsome W.T. (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci. 18, 3870–3896;
- Пространственно-временное моделирование в биологии;
- A. Arieli, A. Sterkin, A. Grinvald, A. Aertsen. (1996). Dynamics of Ongoing Activity: Explanation of the Large Variability in Evoked Cortical Responses. Science. 273, 1868-1871;
- C. v. Vreeswijk, H. Sompolinsky. (1996). Chaos in Neuronal Networks with Balanced Excitatory and Inhibitory Activity. Science. 274, 1724-1726;
- Anatoly Buchin, Sarah Rieubland, Michael Häusser, Boris S. Gutkin, Arnd Roth. (2016). Inverse Stochastic Resonance in Cerebellar Purkinje Cells. PLoS Comput Biol. 12, e1005000;
- David Sussillo, L.F. Abbott. (2009). Generating Coherent Patterns of Activity from Chaotic Neural Networks. Neuron. 63, 544-557;
- A. Renart, J. de la Rocha, P. Bartho, L. Hollender, N. Parga, et. al.. (2010). The Asynchronous State in Cortical Circuits. Science. 327, 587-590.